Diagrama de círculos
Es posible que te hayan recomendado el diagrama de círculos en las asignaturas que tengan que ver con operaciones matemáticas, estadísticas o de lógica, pues son muy útiles para analizar grupos de datos y hasta para tomar mejores decisiones. Es uno de los instrumentos más básicos y efectivos para observar mejor los procesos y sistemas.
Si te ha entrado curiosidad por cual usar no puedes dejar de conocer los principales y cuál es su utilidad, así podrás decidir sin problemas. No dejes de echarle un vistazo a toda la información que traemos en esta oportunidad.
Principales diagramas de círculos
Desde el punto de vista histórico las primeras representaciones gráficas sobre deducciones lógicas se llevaron a cabo por G. Leibniz y luego sus nuevas versiones usadas por G. Boole y A. De Morgan, las cuales formaron la base para que el matemático suizo Leonhard Euler realizara una notación definitiva sobre estas representaciones.
Entonces, uno de los primeros diagramas de círculos conocidos fue el diagrama de Euler el cual hoy en día todavía se emplea para representar las relaciones de inclusión y disyunción en los conjuntos. También están los diagramas de Venn que se usan para representar las relaciones topológicas de unión, inclusión y disyunción entre dos conjuntos.
Los dos tipos de diagrama han sido una gran herramienta para el estudio de matemáticas, lógica de clases y hasta razonamiento diagramático. Ya que permiten representar los conjuntos mediante líneas cerradas, siendo la línea cerrada exterior la que abarca a todos los elementos por eso se conoce como el conjunto universal U.
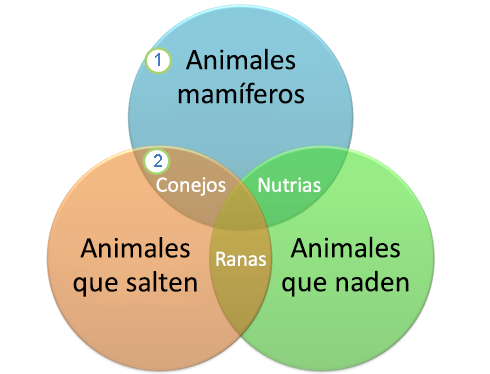
El más empleado es el diagrama de Venn el cual se creó alrededor del año 1880 por John Venn, con la finalidad de representar las relaciones de intersección, inclusión y disyunción sin tener que cambiar la posición relativa de los conjuntos.
¿Qué se representa en el diagrama de círculos de Venn?
Existen diferentes representaciones que se pueden hacer con estos diagramas de círculos, las más usadas son:
- Intersección: esta se usa para representar los elementos que son comunes entre los conjuntos, por ello la región encerrada por sus líneas límite se deben dibujar superpuestas.
- Inclusión: se usa para representar los elementos de un conjunto que forman parte de los elementos de otro, entonces el primero es un subconjunto del segundo, también se puede decir que se encuentra incluido en el segundo.
- Disyunción: se usa en el caso de que los conjuntos no tengan elementos comunes, dejándose la región de superposición vacía.
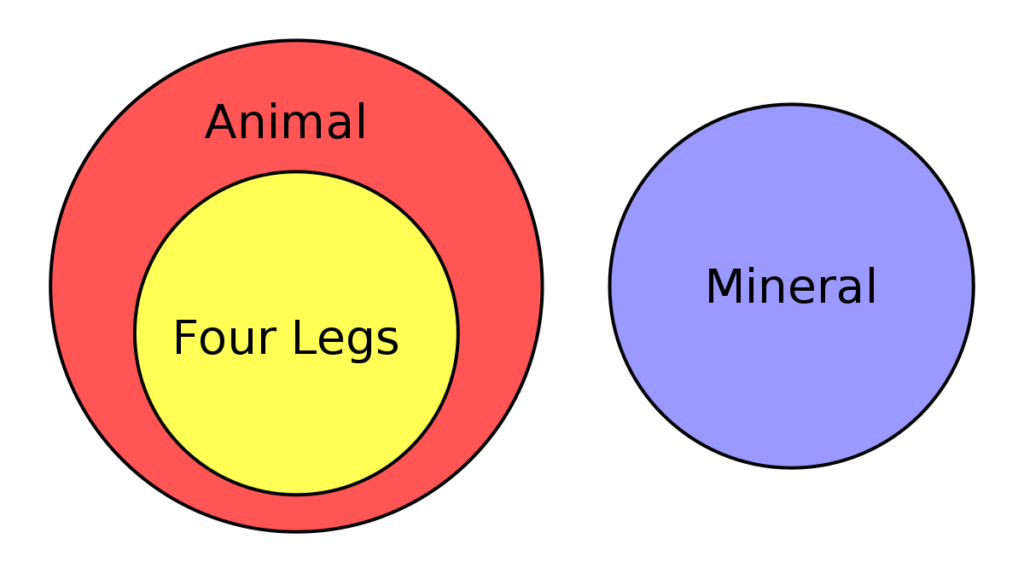
Diferencias entre el diagrama de Euler y de Venn
Existen dos diferencias fundamentales entre estos dos tipos de diagrama:
- En los diagramas de Euler no se muestran las zonas vacías.
- En los diagramas de Euler el conjunto universal no es representado.
Son muchos los beneficios que ofrece emplear este tipo de diagramas pues ayuda a comprender una gran cantidad de relaciones de datos por eso no puedes dejar de profundizar todas sus aplicaciones, así podrás aprovecharlas al máximo.
Si te ha parecido interesante no dejes de compartir la información con tus amigos o en tus redes sociales, seguramente muchas personas querrán aclarar todas estas dudas.
¡Por cierto! Antes de que te vayas, queremos recomendarte esto que seguro que te interesa:
- Diagramas de correlación
- Diagrama de funcionamiento
- Diagrama de instalación eléctrica
- Diagrama de secuencia
- Diagrama de Gowin
- Diagrama de dispersión
- Diagrama de hilos
- Diagrama Otida
- Diagrama de flujo calidad
Son una serie de contenidos a parte del que has leído que puede ser interesante para tí ¡Muchas gracias por leernos!