Diagrama de Euler
La lógica es una de las ramas en las que se divide las matemáticas. A lo largo de los últimos siglos los avances en su estudio han devenido en el desarrollo de una amplia gama de disciplinas como por ejemplo la informática, o la heurística, sin las cuales el mundo simplemente no sería lo que es hoy en día. Gracias al diagrama de Euler, la lógica pudo estructurarse y cimentar sus bases.
El diagrama de Euler puede representarse como una serie de círculos que definen cierto tipo de interacciones entre los conjuntos que forman parte del mismo. Si deseas conocer un poco más acerca de este tema, entonces te invitamos a continuar leyendo este interesante artículo.
¿Qué es un diagrama de Euler?
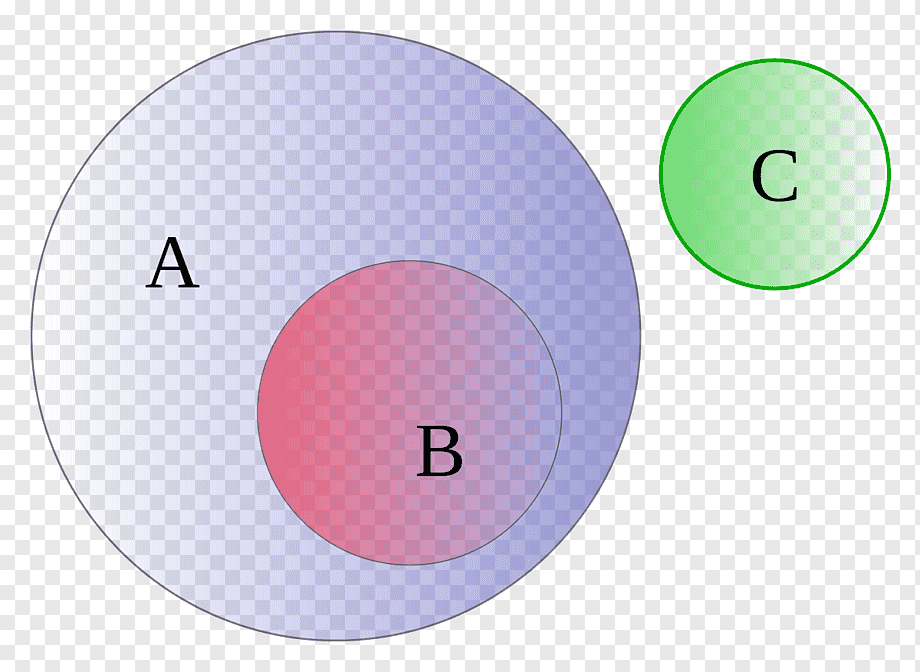
Un diagrama de Euler puede entenderse, al menos desde el punto de vista gráfico, como una serie de curvas cerradas las cuales se encuentran en un plano y que funcionan como un medio para representar cierto tipo de relaciones espaciales como la superposición o la contención, las cuales son especialmente útiles al analizar las funciones de subconjuntos, intersecciones y disjuntes tan características de esta rama de las matemáticas.
Este tipo de diagrama se encarga de llevar a cabo representaciones gráficas en las cuales se incluyen el concepto de conjunto y las diversas relaciones que pueden establecerse entre estos tipos de elementos.
Aunque suele ser comúnmente confundido con los diagramas de Venn, el diagrama de Euler posee sus propias particularidades y se trata más bien de una generalización del mismo. Una de las principales diferencias entre ambos radica en que el diagrama de Euler se encarga de analizar solo el área de interés, mientras que los diagramas de Venn reflejan todas las áreas implicadas.
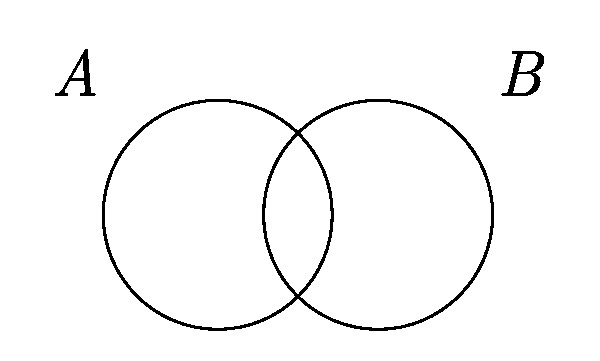
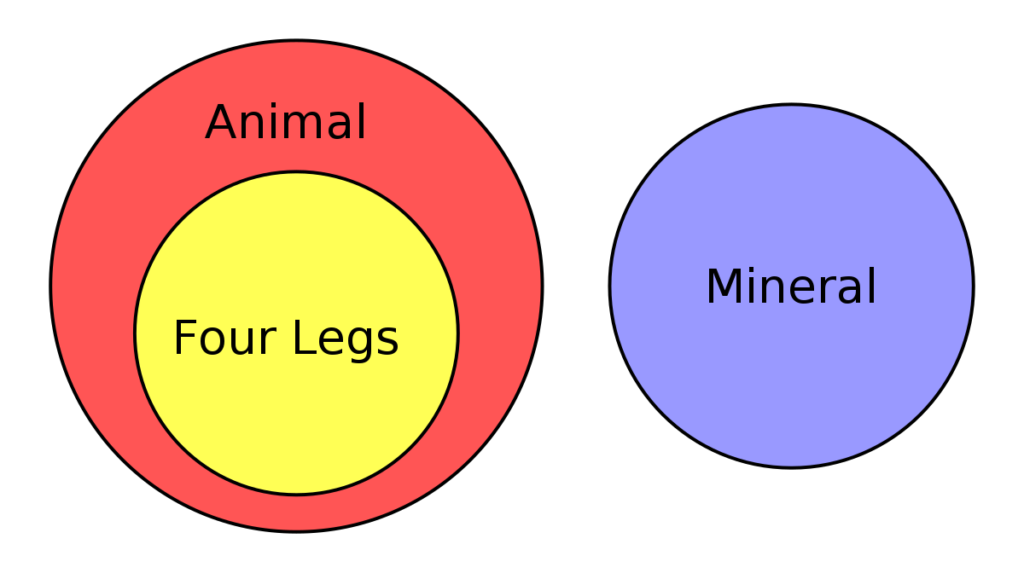
Las zonas en este tipo de diagramas pueden representarse de tal forma que se adapten al tamaño de los conjuntos estudiados, en otras palabras, dichas áreas son directamente proporcionales al tamaño de la muestra. Son ampliamente utilizados por ejemplo para facilitar el estudio de sistemas jerárquicos complejos.
Al tratarse de curvas cerradas en un plano, en muchas ocasiones y dependiendo del fenómeno estudiado, estas curvas se superponen poniendo en evidencia las posibles relaciones que ocurren entre los conjuntos. En este sentido existen si solo se estudian dos conjuntos, entonces solo podrán existir un par de relaciones, de contención y superposición o ninguna de las dos.
Las zonas que se encuentran en la parte interna de la curva son denominadas como elementos del conjunto. Por otro lado, las áreas que están fuera de la curva simplemente no pertenecen al conjunto.
Esperamos que esta información te haya servido para obtener una visión mucho más amplia de diagrama de Euler. Aún hoy en día es considerado como un importante recurso que permite facilitar la comprensión de la teoría de los conjuntos y otras disciplinas relacionadas a la lógica y las matemáticas.
Si el artículo te ha parecido útil e interesante no dudes en compartirlo a través de todas las redes sociales, de esta forma podrás darle una mayor difusión y al mismo tiempo tus familiares y amigos podrán aprovecharlo.
¡Por cierto! Antes de que te vayas, queremos recomendarte esto que seguro que te interesa:
- Diagrama hierro-carbono
- Diagrama pictórico
- Diagrama de Moeller
- Diagrama de colaboración
- Diagrama de Pert
- Diagrama NS
- Diagrama BPMN
- Diagrama de flujo de un servicio
- Diagrama cpm
Son una serie de contenidos a parte del que has leído que puede ser interesante para tí ¡Muchas gracias por leernos!