Diagrama de Hasse
Las matemáticas en incontables ocasiones pasan tristemente desapercibidas a través de nuestras vidas, pues muchas veces somos incapaces de ver el nexo que esta noble ciencia posee con la mayoría de los aspectos que nos rodean en nuestro día a día. Bien sea por ignorancia o simple desconocimiento, decidimos hacernos a un lado dejando de aprovechar todo lo que esta disciplina puede hacer por nosotros.
Más allá de emplear la aritmética en simples cálculos a la hora de estimar el cambio recibido en una compra, un diagrama de Hasse puede utilizarse en áreas del saber como la ingeniería para evaluar indicadores en determinados procesos industriales, o en finanzas al estudiar la viabilidad de un proyecto en particular.
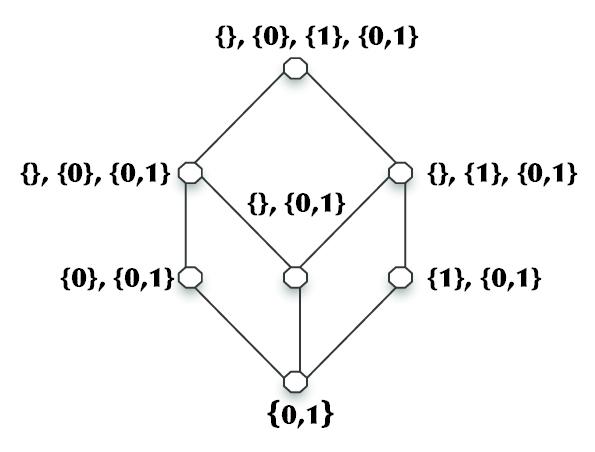
En esta oportunidad podrás descubrir un poco más acerca de esta interesante rama de las matemáticas y aprovechar los diversos aspectos que un diagrama de Hasse pone a tu disposición.
¿Qué es un diagrama de Hasse?
Podemos decir que se trata de una excelente técnica gráfica que se utiliza ampliamente para esquematizar conjuntos parcialmente ordenados. Suele ser muy útil en los casos en los que se desea conocer si existe cierto nivel de jerarquía en los subconjuntos de objetos, al estudiar la posibilidad de definir una relación jerárquica de manera natural y al establecer una técnica que permita realizar satisfactoriamente un proceso de jerarquización canónica.
¿Cómo se crea un diagrama de Hasse?
A continuación, te mostramos de manera general los pasos más básicos que deberás llevar a cabo al momento de crear un diagrama de Hasse:
- Primero que nada, se debe representar cada elemento de un conjunto ordenado como un vértice dentro de nuestra representación gráfica en el plano. Es importante tomar en consideración que se debe trazar una curva o línea recta a partir de cada vértice.
- Las curvas o segmentos de líneas pueden cruzarse entre sí, sin embargo, es necesario tomar en cuenta que no deberán pasar dos veces por los vértices de cada extremo que constituye al diagrama de Hasse.
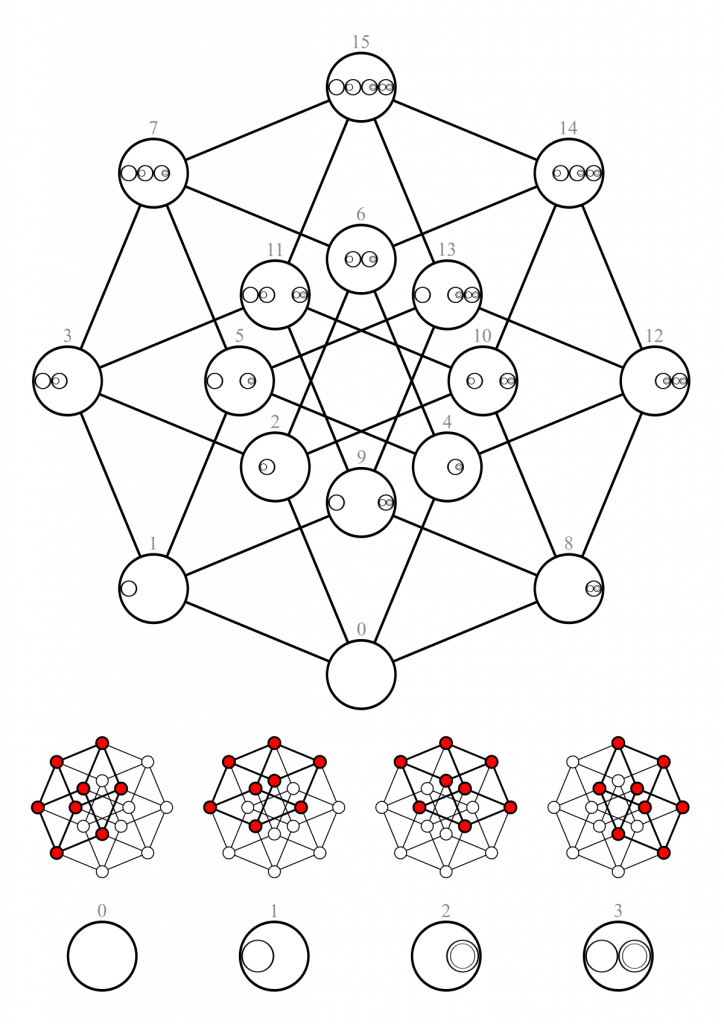
Planariad ascendente en el diagrama de Hasse
Es una de sus principales características y define la viabilidad de este tipo de herramienta. A continuación, te enseñamos algunas de las principales consideraciones que deberás tomar en cuenta al tratarse de la planaridad en un diagrama de Hasse:
- Si los elementos de orden parcial tienen como máximo o mínimo un elemento en común, entonces para poder establecer la relación de planaridad será necesario probar en tiempo lineal que existe un diagrama de Hasse que no se cruza.
- Al momento de realizar una representación de diagrama de Hasse en forma de celosía, es posible graficarla sin la presencia de cruces solo en los casos que el orden parcial tiene un orden máximo de 2.
- Al especificarse la relación de orden parcial con sus coordenadas, entonces también es factible llevar a cabo la representación gráfica sin tener que realizar las cruces.
- Al contarse con un poset de entrada graduado se puede construir un diagrama de Hasse en el que el rango del diagrama es exactamente proporcional a la altura de cada uno de sus vértices.
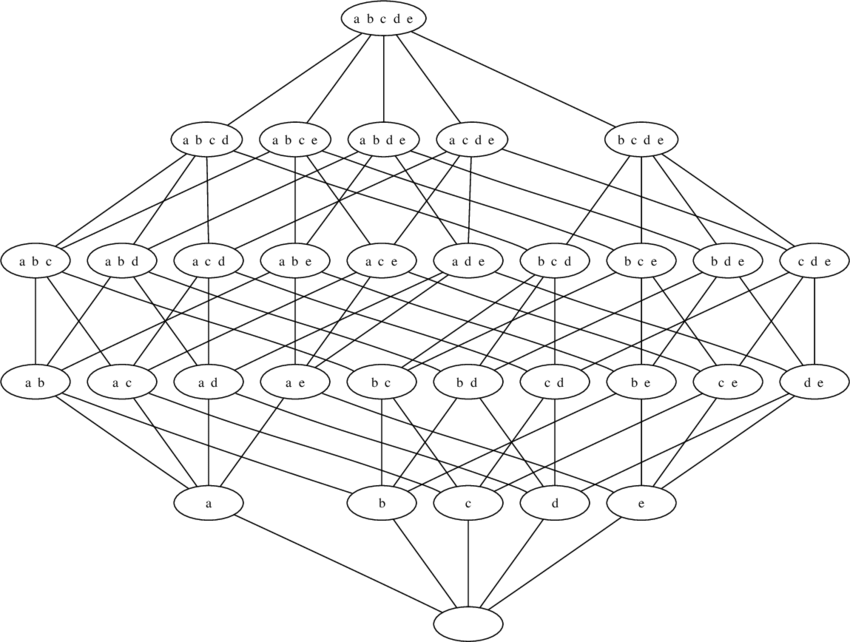
Como podrás haberte dado cuenta el diagrama de Hasse es un potente instrumento que puedes aprovechar al máximo. Si el artículo te ha parecido útil, entonces no dudes en compartirlo.
¡Por cierto! Antes de que te vayas, queremos recomendarte esto que seguro que te interesa:
- Diagrama de dispersión
- Diagrama de Bloom
- Diagrama de datos
- Diagrama de sectores
- Diagrama sinóptico
- Tipos de diagrama
- Diagrama de relevador
- Diagrama CPC
- Diagrama de sankey
Son una serie de contenidos a parte del que has leído que puede ser interesante para tí ¡Muchas gracias por leernos!